|
|
|
|
Een steekproef wordt getrokken uit een populatie U. De omvang van de populatie
wordt aangegeven met N. Als we elk element een volgnummer geven, dan kunnen we
de populatie noteren als een verzameling
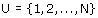
De doelvariabele stelt het verschijnsel voor dat we willen onderzoeken. De
doelvariabele noemen we Y. Hij neemt voor elk element in de populatie een
zekere waarde aan. Die waarden geven we aan met
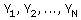
Is de doelvariabele bijvoorbeeld het inkomen van de te onderzoeken personen, dan is
Y1 het inkomen van persoon 1, Y2 het inkomen van persoon 2, enz.
Doel van het onderzoek is het doen van uitspraken over bepaalde karakteristieken van de
doelpopulatie. Zulke karakteristieken worden meestal aangeduid als
populatiegrootheden.
Een belangrijke populatiegrootheid is het populatiegemiddelde. Het
populatiegemiddelde van de doelvariabele Y is gedefinieerd als
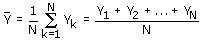
Zou Y het inkomen van een persoon in de populatie aanduiden, dan is het
populatiegemiddelde gelijk aan het gemiddelde inkomen in de populatie.
Doel van het onderzoek kan ook zijn het schatten van het percentage elementen dat een
bepaalde eigenschap heeft. In deze situatie kan de doelvariabele twee mogelijke
waarden aannemen:
- Heeft een element de betreffende eigenschap, dan is de waarde van Y gelijk aan 1;
- Heeft een element de betreffende eigenschap niet, dan is de waarde van Y gelijk aan 0.
Het te schatten populatiepercentage kan dan in formule worden weergegeven als
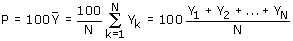
Een andere populatiegrootheid die nog moet worden genoemd, is de populatievariantie. Deze grootheid zegt iets over de mate van variatie van de waarden van de doelvariabele. De populatievariantie is gedefinieerd als
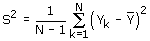
De populatievariantie speelt een belangrijke rol bij het bepalen van de
nauwkeurigheid van schattingen. Deze grootheid kan ook worden opgevat als een
maat voor de homogeniteit van de populatie. Heeft bijvoorbeeld iedereen in de
populatie hetzelfde inkomen, dan is elk inkomen ook gelijk aan het gemiddelde
inkomen. In deze situatie is de populatievariantie dus gelijk aan 0. Naarmate
de inkomensverschillen groter zijn, zal ook de populatievariantie toenemen.
|
|
|
De omvang van de te trekken steekproef geven we aan met n. Een steekproef van omvang n
die is getrokken uit een populatie van omvang N kunnen we aangeven door middel
van een reeks indicatoren
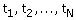
De indicator tk geeft aan of element k uit de populatie is getrokken.
Deze grootheid kan alleen de waarden 0 en 1 aannemen (niet of wel getrokken).
Aangezien de waarden van deze indicatoren het resultaat zijn van de werking van
een kansmechanisme, noemen we ze stochastische variabelen of
kansvariabelen. De steekproefomvang n kan worden teruggevonden
door optellen van de indicatoren:
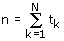
Voor de geselecteerde elementen (dus de elementen met de geselecteerde volgnummers)
meten we de waarde van de doelvariabele. Dit zijn de metingen die in het
steekproefonderzoek beschikbaar komen. De beschikbare metingen geven we aan met
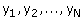
Merk op dat we zoveel mogelijk kleine letters gebruiken voor alles wat met de steekproef te
maken heeft, en hoofdletters voor alles wat betrekking heeft op de populatie.
Dus y1 is de waarde van het eerste element in de steekproef, dus van
de eerste indicator met een waarde groter dan 0.
Voor alle elementen in de steekproef kan de waarde van de doelvariabele worden
waargenomen en vastgelegd.
|
|
|
Voor het trekken van een steekproef moet een lotingsprocedure worden gebruikt. Alleen
dan kunnen de steekproefgegevens worden gebruikt om op verantwoorde wijze
conclusies over de populaties te trekken. Een dergelijke procedure garandeert
dat niemand (bewust of onbewust) wordt bevoordeeld of benadeeld.
Om het lotingsmechanisme op eerlijke en objectieve wijze te kunnen laten werken, is
een soort apparaat nodig. Een dergelijke apparaat heet een aselector. De aselector moet voldoen aan de volgende eigenschappen:
- Het apparaat kan herhaaldelijk worden gebruikt;
- Iedere keer dat het apparaat in werking wordt gesteld geeft het één van de getallen 1
t/m N als uitkomst, waarbij N bekend wordt verondersteld;
- Elke keer opnieuw hebben alle mogelijk uitkomsten dezelfde kansen. Kennis over
eerder uitkomsten helpt niet bij het voorspellen van een volgende uitkomst.
Kortom, elk voorspellingssysteem faalt.
In de praktijk kunnen aselecte getallen op de volgende wijzen worden verkregen:
- Het raadplegen van een tabel met aselecte getallen (voor kleine steekproeven);
- Het gebruik van een rekenmachine (voor kleine steekproeven);
- Het gebruik van een computer(voor grote steekproeven);
Onderstaande tabel bevat een reeks aselecte getallen. De getallen staan bij elkaar in
groepjes van vijf.
| 00822 | 63134 | 04080 | 29373 | 68731 |
34282 | 41827 | 94880 | 11505 | 07677 |
| 79771 | 19758 | 62062 | 81259 | 11215 |
42167 | 70001 | 78364 | 74388 | 10001 |
| 58614 | 41056 | 09869 | 27746 | 12931 |
93018 | 56160 | 39534 | 93340 | 87194 |
| 71287 | 49101 | 03330 | 45468 | 52358 |
62658 | 33674 | 26879 | 17227 | 49102 |
| 12073 | 76580 | 28601 | 14410 | 57528 |
04036 | 28540 | 91001 | 89127 | 94058 |
Stel, er moet een steekproef van 10 leden worden getrokken uit een ledenbestand van een
vereniging die uit 682 leden bestaat. Daarvooer zijn 10 aselecte getallen nodig
uit de reeks van 1 t/m 682. Kies in de tabel een willekeurig beginpunt en nemen
een willekeurige route door de aselecte getallen. Neem bijvoorbeeld steeds drie
opeenvolgende cijfers en zie dat als een getal van drie cijfers. Is dat getal
groter dan 682, negeer het dan en pakn het volgende getal. Is het getal uit de
reeks van 1 t/m 682, dan is dat het volgnummer van een lid dat in de steekproef
komt. Wordt linksboven begonnen, van links naar rechts gegaan, en steeds van
elke groep van vijf cijfers de eerste drie genomen, dan zijn de eerste 10
aselecte getallen:
008, 631, 040, 293, 687, 342, 418, 948, 115, 076, ...
De getallen 687 en 948 zijn groter dan 682, en doen daarom niet mee. De eerste 8
geselecteerde leden zijn dus de leden met volgnummers
8, 631, 40, 293, 342, 418,115 en 76.
Veel programmeertalen en rekenmachines hebben tegenwoordig de mogelijkheid om
aselecte getallen te genereren. Heel vaak is er een routine aanwezig die een
aselecte waarde genereert uit het interval [0, 1). De waarde 0 kan dus voorkomen, maar de waarde 1 net niet. Deze routine kan worden gebruikt voor het trekken van een willekeurig volgnummer uit de reeks 1 t/m N. Dit gaat als volgt:
- Trek een aselecte waarde uit [0, 1).
- Vermenigvuldig die waarde met de populatieomvang N.
- Rond de uitkomst naar beneden af op een gehele waarde.
- Tel bij de uitkomst 1 op.
Zou deze routine op de computer of rekenmachine achtereenvolgens de waarden
0,12073 0,76580 0,28601 0,14410
produceren, dan leidt toepassing van het bovenstaande algoritme voor N = 682 tot de nummers
83, 523, 196, 99
De tabel met aselecte getallen kan ook worden gebruikt in combinatie met het
bovenstaande algoritme. Neem steeds een groepje opeenvolgende cijfers, en zie
dat als het deel achter de komma van een getal tussen 0 en 1. Nemen we de
eerste 4 groepen van vijf cijfers in de eerste rij, dan krijgen we
0,00822 0,63134 0,04080 0,29373
waarna toepassing van het algoritme leidt tot de nummers
6, 431, 28, 201.
De steekproeven moet worden getrokken zonder teruglegging. Dit betekent dat een
element ten hoogste één keer in de steekproef kan worden getrokken. Mocht
toepassing van bovenstaand algoritme ertoe leiden dat een al eerder getrokken
volgnummer nogmaals wordt getrokken, dan moet dit tweede volgnummer worden
genegeerd, en een nieuwe poging worden gedaan.
|
|
|
Voor de geselecteerde elementen (dus de elementen met de geselecteerde volgnummers) kan
de waarde van de doelvariabele worden gemeten. Dit zijn de metingen die in het
steekproefonderzoek beschikbaar komen. De beschikbare metingen geven we aan met
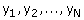
Het zijn deze waarden die moeten worden gebruikt voor het schatten van de
populatiegrootheden. Het recept voor de berekening van een schatting wordt een
schatter genoemd. Bruikbare schatters moeten enkele speciale eigenschappen hebben:
- De schatter moet zuiver zijn. Zou de trekking van de steekproef een groot aantal malen worden herhaald, dan moet het gemiddelde van alle schattingsuitkomsten bij benadering gelijk zijn aan de te schatten waarde van de populatiegrootheid. De eis van zuiverheid garandeert dat de schatter nooit de waarde van de populatiegrootheid systematisch over- of onderschat.
- De schatter moet ook nauwkeurig zijn. Dit houdt in dat de variatie in de mogelijke uitkomsten klein moet zijn. In het ideale geval levert de schatter altijd de juiste waarde op.
Het schatten van een populatiegemiddelde
In het geval van een enkelvoudige aselecte steekproef zonder teruglegging is het
gemiddelde van de steekproefgegevens,
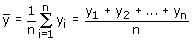
een zuivere schatter voor het populatiegemiddelde. De nauwkeurigheid van deze schatter
wordt gemeten met de variantie van de schatter. Voor een enkelvoudige
aselecte steekproef zonder teruglegging is de variantie van het
steekproefgemiddelde gelijk aan
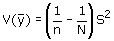
Hierin is
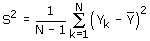
de al eerder genoemde populatievariantie. De schatter is nauwkeuriger naarmate de
variantie kleiner is. De grootte van de variantie wordt door twee factoren
bepaald:
- De populatievariantie. Naarmate de populatie homogener is, zal de schatter nauwkeuriger zijn.
- De steekproefomvang. Naarmate de omvang van de steekproef groter is, zal de schatter nauwkeuriger zijn.
Om iets te kunnen zeggen over de nauwkeurigheid van de berekende schatting, is de waarde
van de variantie nodig. Helaas is die in het algemeen niet bekend, omdat de
variantie-formule de populatievariantie bevat. Deze is gewoonlijk niet bekend.
De oplossing van dit probleem is om de populatievariantie te schatten op basis
van de steekproefgegevens. De steekproefvariantie, gedefinieerd door
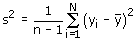
is een zuivere schatter voor de populatievariantie. En dus is
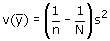
een zuivere schatter voor de variantie van de schatter.
Het schatten van een populatiepercentage
Bij het schatten van een percentage gaat het om het wel of niet hebben van een zeker
kenmerk. Heeft een element het kenmerk wel, dan krijgt de doelvariabele de
waarde 1, en heeft het element het kenmerk niet, dan wordt de waarde van de
doelvariabele 0. Het populatiegemiddelde van deze doelvariabele is dan gelijk
aan de fractie enen, en dus gelijk aan de fractie elementen met dat kenmerk.
Vermenigvuldigen van dat gemiddelde met 100 levert het percentage elementen met
dat kenmerk. Wordt het populatie-percentage aangegeven met de letter P, dan
geldt:
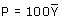
Voor het schatten van dit populatiepercentage
moet eerst het populatiegemiddelde worden geschat. Daarvoor wordt het
steekproefgemiddelde gebruikt. In dit geval is dat gelijk aan de fractie
elementen in de steekproef met het betreffende kenmerk. Vermenigvuldigen van
dit steekproefgemiddelde met 100 geeft het steekproefpercentage. Dit wordt
aangegeven met
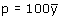
Aangezien het steekproefgemiddelde een zuivere schatter is voor het populatiegemiddelde,
is het steekproefpercentage een zuivere schatter voor het populatiepercentage.
De variantie van het steekproefpercentage is gelijk aan
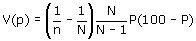
Deze variantie kan worden geschat op basis van de steekproefgegevens met behulp van
de formule
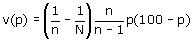
Betrouwbaarheidsinterval
Het is niet eenvoudig om de berekende waarde van de variantie te interpreteren in termen van betrouwbaarheid. Een beter middel hiervoor is het betrouwbaarheidsinterval. Als
eerste stap hiervoor moet de standaardfout van de schatter worden berekend.
Deze is gelijk aan
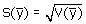
Deze standaardfout kan worden geschat door in deze formule de populatie-variantie te
vervangen door de schatter voor de populatievariantie:
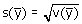
Het betrouwbaarheidsinterval wordt gekenmerkt door een onder-
en een bovengrens die zijn bepaald op grond van de beschikbare gegevens, en wel
zo dat de kans dat dit interval de (onbekende) populatiewaarde bevat, minstens
gelijk is aan een van te voren vastgestelde (grote) kans 1 - α
De grootheid 1 - α wordt de betrouwbaarheid genoemd.
Vaak wordt voor α de waarde 0,05 gekozen. Daaruit volgt dat de
betrouwbaarheid dan gelijk is aan 0,95. De betekenis daarvan is de volgende:
als de steekproeftrekking en de berekening van de schatting een groot aantal
malen zou worden herhaald, dan zou in gemiddeld 95 van de 100 gevallen het
betrouwbaarheidsinterval de te schatten populatiewaarde bevatten.
Als dus de uitspraak wordt gedaan dat het betrouwbaarheidsinterval de onbekende
populatiewaarde bevat, dan is die inspraak in gemiddeld 5% van de gevallen een
onjuiste uitspraak. Anders geformuleerd: de onderzoeker loopt het risico in
gemiddeld 1 op de 20 gevallen een verkeerde uitspraak te doen.
De keuze van de betrouwbaarheid is in principe vrij. Is een uitspraak met een hoge
betrouwbaardheid vereist, dan moeten de waarde van α kleiner worden genomen. Een waarde α=0,01 zou bijvoorbeeld kunnen worden overwogen. Daarvoor moet wel een prijs worden betaald. Die prijs is dat het resulterende betrouwbaarheidsinterval groter zal zijn. Er is in feite sprake van een uitruil tussen betrouwbaarheid en nauwkeurigheid: òf er wordt een minder nauwkeurige uitspraak met een grote betrouwbaarheid gedaan, òf een nauwkeurige uitspraak met een minder grote betrouwbaarheid.
De grenzen van het betrouwbaarheidsinterval zijn betrekkelijk eenvoudig te bepalen. Het
midden van het interval is de waarde van de schatting zelf (dus het steekproefgemiddelde, of het steekproefpercentage). Daarbij wordt een bepaalde marge M opgeteld voor de bovengrens, en aftrekken van de marge geeft de ondergrens. Die marge is gelijk aan de standaardfout van de schatter, vermenigvuldigd met een constante. Voor een betrouwbaarheid van 0,95 is deze constante gelijk aan 1,96.
Voor het schatten van het populatiegemiddelde wordt het 95%-betrouwbaarheidsinterval
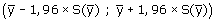
Voor het schatten van het populatiepercentage wordt het 95%-betrouwbaarheidsinterval
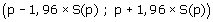
In de praktijk is de standaardfout niet bekend. Daarom wordt deze grootheid in de
formule vervangen door de schatter van de standaardfout.
|
|
|
Aan het begin van een onderzoek komt altijd de vraag op hoe groot de omvang van de
steekproef moet zijn? Deze (nu nog onbekende) omvang wordt genoteerd met n.
Er kan geen eenduidig antwoord op deze vraag worden gegeven. Er is een verband tussen de
omvang van de steekproef en de nauwkeurigheid van de uitspraken die over de
populatie kunnen worden gedaan. Hoe groter de steekproef, des te nauwkeuriger
de uitspraken.
Steekproefomvang voor het schatten van een gemiddelde
De eis dat de marge niet groter mag zijn dan een zekere waarde M, kan worden vertaald in
de relatie
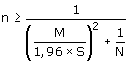
Voor grote waarden van N kan de formule worden vereenvoudigd tot
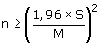
Probleem bij beide formules is dat de waarde van (de wortel uit) de populatievariantie
in veel gevallen niet bekend is. Soms kan een schatting worden gemaakt op grond
van voorgaand onderzoek, of misschien is er een indicatie van de waarde uit een
proefonderzoek. Dan kan deze waarde worden ingevuld.
Als er totaal geen indicatie is voor de waarde van S, dan kunnen de volgende
vuistregels eventueel uitkomst bieden:
- De waarden van de doelvariabele zijn min of meer normaal verdeeld over een interval van bekende lengte L.
Dan zal L ongeveer gelijk zijn aan 6S, en kan voor S dus de waarde 0,17 L worden ingevuld.
- De waarden van de doelvariabele zijn gelijkmatig verdeeld over een interval van bekend lengte L.
Dan zal S ongeveer gelijk zijn aan 0,3 L.
- De waarden van de doelvariabele zijn ongeveer exponentieel verdeeld over een interval van bekend lengte. Dat betekent dat er heel veel kleine waarden zijnn en heel weinig grote
waarden. Dan zal S ongeveer gelijk zijn aan 0,4 L.
- De meest ongunstige situatie wordt verkregen als de heflt van de waarden zich bevindt aan het linker uiteinde van het interval van lengte L, en de andere helft van de waarden
aan het rechter uiteinde van het interval. In dit geval is S gelijk aan 0,5 L.
Steekproefomvang voor het schatten van een percentage
Laat M de maximaal toe te laten marge zijn tussen de werkelijke (maar onbekende) waarde
van het populatiepercentage P en de schatting daarvan op basis van de
steekproef.
Een waarde van M=2 betekent bijvoorbeeld dat een afwijking van meer dan 2 procentpunten
niet is toegestaan. Dan kan de bijbehorende steekproefomvang n worden
uitgerekend via de formule:
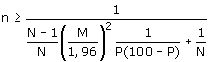
In principe is P onbekend, want die waarde moet juist worden geschat. Soms is er echter een
ruwe indicatie van P bekend uit vorig of ander onderzoek. Die indicatie moet
dan worden ingevuld. Is er echt helemaal niets bekend over P, vul dan voor P de
waarde 50 in. Dit levert een steekproefomvang die in ieder geval nauwkeurig
genoeg is.
Voorbeeld 1:
Populatie van N = 40 000, P = 50, M = 3 (afwijking niet groter dan 3%):
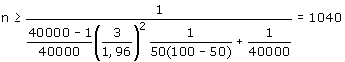
Voorbeeld 2:
Populatie van N = 400, P = 50, M = 5 (afwijking niet groter dan 5%):
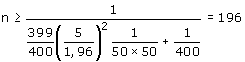
Benadering 1:
Als de populatieomvang N erg groot is, zeg N > 10000, dan kan de formule worden
vereenvoudigd tot
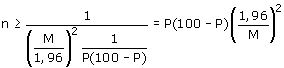
Benadering 2:
Als de populatieomvang N erg groot is, zeg N > 10000, en P is helemaal onbekend dan
kan de formule worden vereenvoudigd tot
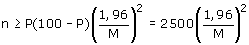
|
 |
|

